Computer and art mix very nicely. We can algorithmically generate patterns, be it pictures or music, which are aesthetic.

Here is an example program for *nix systems which generates fractal like tiling. We use tga format, which is simple but uncompressed. For compression, we may use imagemagick suit's convert command.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

#include <stdio.h>
#include <fcntl.h>
#include <math.h>
#include <stdlib.h>
#include <unistd.h>

#define width 1366
#define height 768

char pic[height][width][3];

int main(){
  unsigned int i,j;
  int fd;
  char buffer[100];

  for (i=0; i<height; i++)
    for (j=0; j<width; j++){
    pic[i][j][0] = 0;
    pic[i][j][1] = 0;
    pic[i][j][2] = (((i^(~j))&((~i-350)>>3)))&255;
    }

  if ((fd = open("image.tga", O_RDWR+O_CREAT, S_IRUSR | S_IWUSR)) == -1)
  {
    printf("error opening file\n");
    exit(1);
  }
  buffer[0] = 0;
  buffer[1] = 0;
  buffer[2] = 2;
  buffer[8] = 0;
  buffer[9] = 0;
  buffer[10] = 0;
  buffer[11] = 0;
  buffer[12] = (width & 0x00FF);
  buffer[13] = (width & 0xFF00) >> 8;
  buffer[14] = (height & 0x00FF);
  buffer[15] = (height & 0xFF00) >> 8;
  buffer[16] = 24;
  buffer[17] = 0;
  write(fd, buffer, 18);
  write(fd, pic, width*height*3);
  close(fd);
  return 0;
}

The same program can be written in python too, easier to write, but slower in execution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

WIDTH = 1366
HEIGHT = 768

header = [0]*18
header[0] = 0
header[1] = 0
header[2] = 2
header[8] = 0
header[9] = 0
header[10] = 0
header[11] = 0
header[12] = (WIDTH & 0x00FF)
header[13] = (WIDTH & 0xFF00) >> 8
header[14] = (HEIGHT & 0x00FF)
header[15] = (HEIGHT & 0xFF00) >> 8
header[16] = 24
header[17] = 0

if __name__ == "__main__":
    ba = bytearray()

    for i in xrange(HEIGHT):
        for j in xrange(WIDTH):
            blue = 0
            green = 0
            red = (((i ^ (~j)) & ((~i - 350) >> 3))) & 255
            ba.extend(bytearray([blue, green, red]))

    with open("imagepy.tga", "w") as fd:
        fd.write(bytearray(header))
        fd.write(ba)

Image generated by the program

Reading the disassembled code from the C programs which we can comfortably write is a great way to learn assembly language, do some archtecture specific optimizations and also to know what's happening under the hood.

In this post, we will see how to translate a small C program to assembly (using flat assembler).

Consider the following, where the code for gcd is taken from rosetta code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

#include <stdio.h>

int gcd(int u, int v) {
    return (v != 0)?gcd(v, u%v):u;
}

int main() {
    int n,m;
    scanf("%d%d",&n,&m);
    printf("%d \n",gcd(n,m));
    return 0;
}

Compile to 32 bit code as

1

gcc -o gcd gcd.c -m32

and disassemble:

1
2

gdb ./gcd
(gdb) disas gcd

We will see something like this:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

0x08048454 <+0>  :    push   ebp
0x08048455 <+1>  :    mov    ebp,esp
0x08048457 <+3>  :    sub    esp,0x18
0x0804845a <+6>  :    cmp    DWORD PTR [ebp+0xc],0x0
0x0804845e <+10> :    je     0x804847e <gcd+42>
0x08048460 <+12> :    mov    eax,DWORD PTR [ebp+0x8]
0x08048463 <+15> :    mov    edx,eax
0x08048465 <+17> :    sar    edx,0x1f
0x08048468 <+20> :    idiv   DWORD PTR [ebp+0xc]
0x0804846b <+23> :    mov    eax,edx
0x0804846d <+25> :    mov    DWORD PTR [esp+0x4],eax
0x08048471 <+29> :    mov    eax,DWORD PTR [ebp+0xc]
0x08048474 <+32> :    mov    DWORD PTR [esp],eax
0x08048477 <+35> :    call   0x8048454 <gcd>
0x0804847c <+40> :    jmp    0x8048481 <gcd+45>
0x0804847e <+42> :    mov    eax,DWORD PTR [ebp+0x8]
0x08048481 <+45> :    leave
0x08048482 <+46> :    ret

and

1

(gdb) disas main

shows like this:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

0x08048483 <+0>  :    push   ebp
0x08048484 <+1>  :    mov    ebp,esp
0x08048486 <+3>  :    and    esp,0xfffffff0
0x08048489 <+6>  :    sub    esp,0x20
0x0804848c <+9>  :    mov    eax,0x80485b0
0x08048491 <+14> :    lea    edx,[esp+0x1c]
0x08048495 <+18> :    mov    DWORD PTR [esp+0x8],edx
0x08048499 <+22> :    lea    edx,[esp+0x18]
0x0804849d <+26> :    mov    DWORD PTR [esp+0x4],edx
0x080484a1 <+30> :    mov    DWORD PTR [esp],eax
0x080484a4 <+33> :    call   0x8048380 <__isoc99_scanf@plt>
0x080484a9 <+38> :    mov    edx,DWORD PTR [esp+0x1c]
0x080484ad <+42> :    mov    eax,DWORD PTR [esp+0x18]
0x080484b1 <+46> :    mov    DWORD PTR [esp+0x4],edx
0x080484b5 <+50> :    mov    DWORD PTR [esp],eax
0x080484b8 <+53> :    call   0x8048454 <gcd>
0x080484bd <+58> :    mov    edx,0x80485b5
0x080484c2 <+63> :    mov    DWORD PTR [esp+0x4],eax
0x080484c6 <+67> :    mov    DWORD PTR [esp],edx
0x080484c9 <+70> :    call   0x8048390 <printf@plt>
0x080484ce <+75> :    mov    eax,0x0
0x080484d3 <+80> :    leave
0x080484d4 <+81> :    ret

From the disassembly, we can see that the function arguments are pushed from right to left. We can also see that the local variables are allocated space in the stack.

We need to replace all the relative references by labels, memory references by names and remove all "PTR" keywords. Using the example to produce dynamically linked executable from fasm for linux (doing it in 1.70.03), we may write it as:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

format ELF executable 3
entry start

include      'examples/elfexe/dynamic/import32.inc'
include      'examples/elfexe/dynamic/proc32.inc'

interpreter  '/lib/ld-linux.so.2'
needed       'libc.so.6'
import       printf,scanf,exit

segment readable executable

gcd:
    push   ebp
    mov    ebp,esp
    sub    esp,0x18
    cmp    DWORD [ebp+0xc],0x0
    je     l1
    mov    eax,DWORD [ebp+0x8]
    mov    edx,eax
    sar    edx,0x1f
    idiv   DWORD [ebp+0xc]
    mov    eax,edx
    mov    DWORD [esp+0x4],eax
    mov    eax,DWORD [ebp+0xc]
    mov    DWORD [esp],eax
    call   gcd
    jmp    l2
l1:
    mov    eax,DWORD [ebp+0x8]
l2:
    leave
    ret

start:
    push     ebp
    mov      ebp,esp
    and      esp,0xfffffff0
    sub      esp,0x20
    cinvoke  scanf,pars,n,m
    mov      edx,[n]
    mov      eax,[m]
    mov      DWORD  [esp+0x4],edx
    mov      DWORD  [esp],eax
    call     gcd
    cinvoke  printf,parspf,eax
    mov      eax,0x0
    cinvoke  exit

segment readable writeable
    pars    db '%d%d',0
    parspf  db '%d',0xa,0
    n       dd 0
    m       dd 0

and assemble:

1

./fasm gcd.asm

The assembled code will perform the same way, but the executable produced is about 10 times smaller! With the assembly code, we will have more liberty to use architecture specific instructions. And, if we see that there are unnecessary register spills happening, we may modify the code to avoid it. (using "register" keyword and -O3 option in gcc makes good use of registers)

p.s.

• By default, disassembly syntax is not intel. To change it, use

  1	set disassembly-flavor intel

  You may consider placing it in $HOME/.gdbinit to use intel syntax everytime.

• -m32 option in gcc is not required if 32 bit linux distro is used.

• -g option is helpful in debugging the executable. We can check instruction-wise disassembly and also deduce the operator precedence. You'll never need another silly book on C. When in doubt, go to the root!

Suppose there is an array of lights, initially all turned off, and during each step you randomly select a light and turn it on or off if it's in off or on state, respectively. On an average, how many steps are required to take it to all turned on state?

This can be solved using an absorbing Markov chain, or by using a probability tree diagram.

In the method using the absorbing Markov chain, the starting state is for all turned off. It can move to the next state which is for one random light turned on. The probability of moving to that state is 1.

From state 1, it can go back to state 0 with a probability of \(\dfrac{1}{n}\), or to state 2 with probability of \(1-\dfrac{1}{n}\).

And so on, in the \((n-1)^{th}\) state, it can go to the absorbing state n with a probability of \(\dfrac{1}{n}\).

E.g. For \(n=6\), the matrix looks like this:

Thus, the matrix Q is:

And the Expected number of steps is found from

The sum of first row gives the expected time it takes to move from the initial state to the absorbing state, which evaluates to \(\dfrac{416}{5} = 83.2\) steps.

This markov chain can be used also to calculate the probability of being in a certain state after 'k' steps.

E.g. What is the probability of all 6 lights being turned on after random flipping of switches 8 times?

Answer is \(A^8[0,6] = \dfrac{215}{5832}\)

We can construct the markov chain and calculate the expected value in Sagemath (a very promising free CAS) as follows:

1
2
3
4
5
6
7
8
9

n=6
mx=[[0]*(n+1) for i in range(n+1)]
mx[0][1]=1
for i in range(1,n):
    mx[i][i-1]=i/n
    mx[i][i+1]=1-i/n
mx[n][n]=1
am=matrix(mx)
print sum((identity_matrix(n)-am[0:n,0:n]).inverse()[0].list())

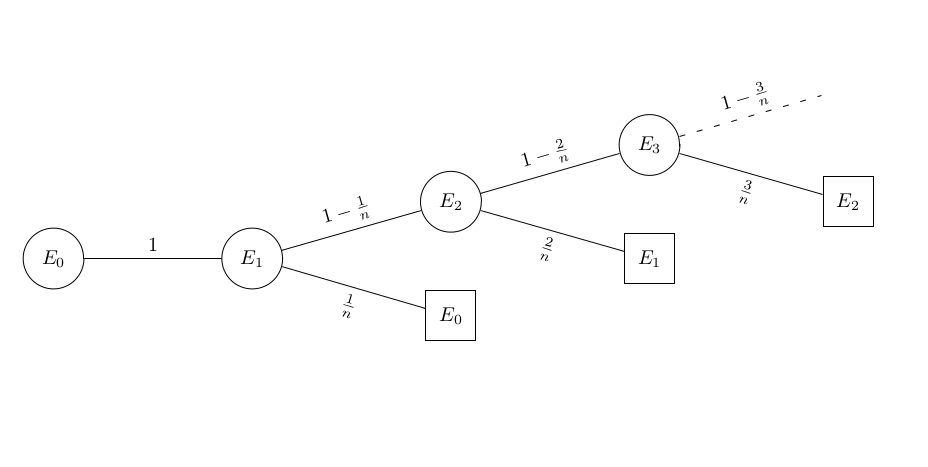
If we want to know only the expected value, we can use the tree method:

Probability tree to calculate expected value

From the above set of equations, we can derive the following algorithm to calculate the expected value in Sage:

1
2
3
4
5
6
7
8
9

ax = 1
n = 6
summ = 0
i = 0
while i<n:
    ax = (ax*i+x)/(x-i)
    summ += ax
    i+=1
print summ.subs(x=n)

As we see, the n is taken to be \(6\), and the answer returned is \(416/5\). The variable name is chosen as 'summ', since sum is a function's name. And, ax indicates a function of x.

For higher values of n, we get e.g.

\(n=32:\)

\(n=64:\)

It all started when the lightning struck and disrupted the internet service. Previously, the settings were stored in the router itself, but after the incident it was no longer connecting to the ppp server.

I called the ISP, and the router's configuration was changed by the support guy and since he's familiar only with windoze, I had to reboot it to windows xp (which I no longer use, only linux based OS now). Now, in order to connect to the internet, the username/password needs to be given in the dial-up prompt for the broadband connection (pppoe). But, for some weird reason, DNS was working, but no ping reply from any sites!

So I decided to try in linux mint, and thought of using pppoeconf.

It's straight-forward, for my ISP's connection the default settings worked. The only information which I needed to change was the username/password

To my surprise, ping replies were okay, but the DNS look up was not working now. After tinkering around with the files in /etc/ppp and reading some man pages related to ppp, I discovered an info referring to /etc/resolv.conf file. But, there was no such file in /etc by default.

So, I copied the /etc/ppp/resolv.conf to /etc

Surprise again, it was still not working. Then I tried strace nslookup google.com

Somewhere near the end of the output, I found open("/etc/resolv.conf", O_RDONLY) = -1 EACCES (Permission denied). So, sudo chmod 0644 /etc/resolv.conf, and rebooted the system.

Everything worked fine after that.

Update: Actually, we need not worry about configuring from the terminal at all. With network manager already there, we just need to go to "network connections"->"DSL" in the menu, and add our connection id/passwd.