Animations with Context Free Art

Context Free Art can also be used to create animations, and here let's see how to generate some moire patterns.

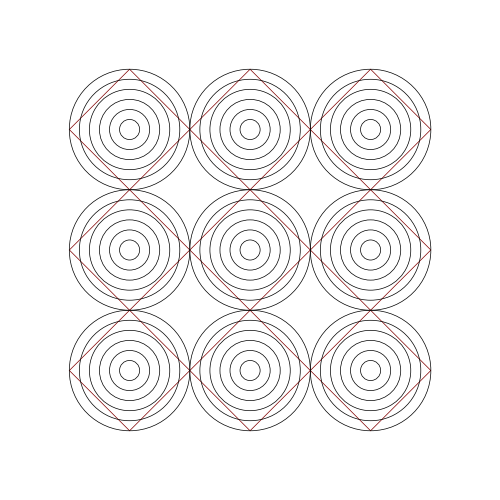
To generate each frame, cfdg uses the time parameter, and the ftime() function gets the value for that frame. For our first example, we generate moire patterns with circles.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
 
startshape start

CF::Time = [time -2 2]
CF::Background = [b 1]
CF::Size = [s 3]

path circ(number rad) {
    MOVETO(rad,0)
    ARCTO(-rad,0,rad, CF::ArcCW)
    ARCTO(rad,0,rad, CF::ArcCW)
    STROKE(0.01)[]
}

shape moire {
    loop 70 [s 0.98]
        circ(1)[]
}

shape start {
    moire[x ftime() time -2 2 s 1]
    moire[x -ftime() time -2 2 s 1]
}

To compile and generate the video of the animations

1
 
cfdg moire_circles.cfdg -s 1080 -a 15x25 -o ta%f.png

generates 375 images (15 seconds, 25 fps) for the animation

1
 
ffmpeg -r 25 -i ./ta%3d.png -c:v libx264 out.mp4

creates the HD video having a frame rate of 25.

And here's the final output

Similarly, we can create a couple more animations like moire patterns by rotating grates and rotating two graphene layers

Optical Illusions with Context Free Art

Context Free Art is a program to generate images using context free grammar. We can obtain beautiful images by writing a few tens of lines of code.

To make it more interesting, let's write code for Optical Illusions. There's a nice list already done using LaTeX, below are translations and output of some of those.

CFDG uses startshape to know which shape to call first. Then the startshape can use other shapes or paths (primitive symbols, user defined).

Read the documentation for details and examples.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
 
startshape start

CF::Background = [hue 90 sat -0.5 b -0.5]
CF::Size = [s 15]

shape start {
    loop j=6 [] {
    rad = 28 + j*14
    twist = (-1)^j * 12
        loop i=rad [] {
            xs = (j + 2)*cos(i*360/rad)
            ys = (j + 2)*sin(i*360/rad)
            rota = i*360/rad + twist
            if (mod(i, 2) == 1) {
                sq [b 1 x xs y ys r rota]
            } else {
                sq [b -1 x xs y ys r rota]
            }
        }
    }
}

path sq {
    MOVETO(0, 0)
    LINETO(0, 0.3)
    LINETO(0.3, 0.3)
    LINETO(0.3, 0)
    LINETO(0, 0)
    STROKE(0.03)[]
}
../../images/sqr_circles.png

Illusion 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
 
startshape start

CF::Background = [hue 90 sat -0.5 b -0.5]
n = 8
xt = (n - 1)/2
yt = (n - 1)/2
scale = n + 2
CF::Size = [s scale x -xt y -yt]
sqd = 0.8                 // square size
circd = sqrt(2)*(1 - sqd) // circle size

shape start {
    loop j=n [] {
        loop i=n [] {
            ys = j + 0.5
            xs = i + 0.5
            SQUARE[b -1 s sqd x i y j]
            if (i < n-1 && j < n-1) {
                CIRCLE[z 1 b 1 s circd x xs y ys]
            }
        }
    }
}
../../images/grid.png

Illusion 2

Output of illusions three, four, and five are shown below

../../images/circles_lines.png

Illusion 3

../../images/floor_tiles.png

Illusion 4

../../images/grid_lines.png

Illusion 5

These examples only used simple loops, more complicated shapes can be drawn using recursion. Check out the CFDG gallery for more examples.

Perfect Parity Patterns

When image data is involved, the results can be engrossing even if there are bugs in our code.
                                                                                       - D. E. Knuth, TAOCP Vol. 4A

A parity pattern is a binary matrix where each entry is the xor of its adjacent neighbors (horizontal or vertical). It's called perfect when there's no row or column consisting of entirely zeroes.

We can build bigger parity patterns from smaller ones, which reveals nice fractals when they are plotted as a bitmap.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
 
def build_matrix(nbits=5):
    cnt = 0
    for a in range(1, 2^(nbits-1)):
        con = true                    # continue with the plotting process
        nn = nbits
        b = Integer(a)
        c = b.bits()
        c = c + [0]*nbits

        am = matrix(ZZ, [c[:nbits]]).stack(zero_matrix(nbits-1, nbits))
        zmv = zero_matrix(ZZ, nn, 1)
        zmh = zero_matrix(ZZ, 1, nn+2)
        am = zmv.augment(am).augment(zmv)
        am = zmh.stack(am).stack(zmh) # consider values outside matrix as 0

        if am[1, :ceil(am.ncols()/2)].list() != am[1, floor(am.ncols()/2):].list()[::-1]:
            continue                  # Let's have vertical symmetry (palindrome check)

        for i in range(2,nn+1):
            for j in range(1,nn+1):
                am[i, j] = (am[i-1, j-1] ^^ am[i-1, j] ^^ am[i-1, j+1] ^^ am[i-2, j])

        for j in range(1, nn):
            if am[nn, j] != am[nn-1, j] ^^ am[nn, j-1] ^^ am[nn, j+1]:
                con = false           # is the computed matrix actually a parity pattern?
                break

        if not con:
            continue

        cnt += 1

        nn1 = 2*nn+2
        while nn < 200:               # build 383x383 matrices
            nn1 = 2*nn+2
            bn = zero_matrix(ZZ, nn1)
            for i in range(nn+1):
                for j in range(nn+1):
                    bn[2*i, 2*j] = am[i, j]
                    bn[2*i+1, 2*j] = am[i, j] ^^ am[i+1, j]
                    bn[2*i, 2*j+1] = am[i, j] ^^ am[i, j+1]
                    bn[2*i+1, 2*j+1] =  0
            bn = bn.delete_rows([0]).delete_columns([0])
            nn = nn1 - 1
            zmv = zero_matrix(ZZ, nn, 1)
            zmh = zero_matrix(ZZ, 1, nn+2)
            am = bn
            am = zmv.augment(am).augment(zmv)
            am = zmh.stack(am).stack(zmh)
        mp = matrix_plot(bn, frame=False)
        mp.show()
    print cnt

build_matrix(11)

And we get a bunch of fractals

../../images/sageR.jpg

Patterns

Source:

Exercises 190 & 193, 7.1.3, Donald E. Knuth, The Art of Computer Programming, Vol. 4A

Generating Music With SageMath And Sonic Pi - Examples - 2

1 Blues Loop

An approximate translation of the Blues Loop illustrated at mathematica.SE. (Listen to the Blues Loop)

Sync the OSC URL in Sonic Pi

1
2
3
4
5
6
7
8
 
live_loop :foo do
  use_synth :piano
  use_real_time
  p1, p2, p3, t1, t2 = sync "/osc/trigger/play"
  play :C, pitch: p1, attack: t1, attack_level: 0, sustain: t2-t1, release: t2-t1
  play :C, pitch: p2, attack: t1, attack_level: 0, sustain: t2-t1, release: t2-t1
  play :C, pitch: p3, attack: t1, attack_level: 0, sustain: t2-t1, release: t2-t1
end

And send the notes from Sage

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
 
%python
import numpy as np
import OSC
from time import sleep

addr = ('localhost', 4559)
cl = OSC.OSCClient()
cl.connect(addr)

def send_message(url, *args):
    msg = OSC.OSCMessage()
    msg.setAddress(url)
    for l in args:
        msg.append(l)
    cl.send(msg)

c = 1.25
v = np.array([0, 0.4], dtype=float)
b = 0.25
lst = [[-12, -5, 0], [-8, -3, 4], [-5, -13, 2], [-3, 0, -8], [-2, -12, -8], [-3, 0, -8], [-5, -1, 2], [-8, -3, -20]]
li = np.array(lst, dtype=int)

def bld(l1, rep):
    for r in range(rep):
        for l in l1:
            for p in v/c:
                dur = np.array([p, p+b], dtype=float)/c
                send_message("/trigger/play", l, dur)
                sleep(dur[1])

li2 = [[li, 1], [li + 5, 1], [li, 2], [li + 5, 2], [li, 2], [li + 7, 1], [li + 5, 1], [li, 1], [li + 7, 1]]

for l in li2:
    bld(l[0], l[1])

2 Morse Code

Let's make a dynamic worksheet to generate morse code beeps. Only alpha-numeric symbols are used here, and timings are taken from a Sonic Pi example

In Sonic Pi,

1
2
3
4
5
6
7
8
 
live_loop :foo do
  use_synth :saw
  use_real_time
  t1, t2 = sync "/osc/trigger/morse"
  cue t1, t2
  play :C6, sustain: t1*0.9, release: t2*0.1
  sleep t1
end

and in SageMath,

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
 
%python
import numpy as np
import OSC
from time import sleep

addr = ('localhost', 4559)
cl = OSC.OSCClient()
cl.connect(addr)

def send_message(url, *args):
    msg = OSC.OSCMessage()
    msg.setAddress(url)
    for l in args:
        msg.append(l)
    cl.send(msg)

codes = {
    'A': '.-',     'B': '-...',   'C': '-.-.',
    'D': '-..',    'E': '.',      'F': '..-.',
    'G': '--.',    'H': '....',   'I': '..',
    'J': '.---',   'K': '-.-',    'L': '.-..',
    'M': '--',     'N': '-.',     'O': '---',
    'P': '.--.',   'Q': '--.-',   'R': '.-.',
    'S': '...',    'T': '-',      'U': '..-',
    'V': '...-',   'W': '.--',    'X': '-..-',
    'Y': '-.--',   'Z': '--..',   '0': '-----',
    '1': '.----',  '2': '..---',  '3': '...--',
    '4': '....-',  '5': '.....',  '6': '-....',
    '7': '--...',  '8': '---..',  '9': '----.'
}

speed = 0.08
code_timing = {'.': 1*speed, '-': 3*speed}
element_gap = 1*speed
char_gap = 3*speed
word_gap = 7*speed - char_gap

def to_morse_code(s):
    spl = s.split(' ')
    for l in spl:
        if l == '': continue # if multiple spaces are input
        mc = ' '.join(codes.get(i.upper()) for i in l)
        print l + ": " + mc

    for c in s:
        if c == ' ':
            sleep(word_gap)
            continue
        mc = codes.get(c.upper())
        for i in mc:
            send_message("/trigger/morse", code_timing[i], code_timing[i])
            sleep(element_gap + code_timing[i])
        sleep(char_gap + element_gap)


@interact
def _( msg=input_box(label='Enter Message', type=str, default='Hi'), auto_update=True):
    to_morse_code(msg)