How many n-digit numbers are there which do not contain 122 and 213 in them? Numbers start with a nonzero digit.

We can write a directed graph to solve that, the weighted adjacency matrix for which is given by:

\begin{equation*} \displaystyle D = \left(\begin{array}{ccccccc} & I & A & 1 & 2 & 12 & 21 \\ I & 0 & 7 & 1 & 1 & 0 & 0 \\ A & 0 & 8 & 1 & 1 & 0 & 0 \\ 1 & 0 & 8 & 1 & 0 & 1 & 0 \\ 2 & 0 & 8 & 0 & 1 & 0 & 1 \\ 12 & 0 & 8 & 0 & 0 & 0 & 1 \\ 21 & 0 & 7 & 1 & 0 & 1 & 0 \end{array}\right) \end{equation*}

'I' is the initial state, '1' and '2' are the states if those digits are the last encountered. \(A\) is for any other valid digits. It goes to state \(12\) or \(21\) if we see a sequence of 12 or 21, respectively. The number of ways of valid transitions are given as the weights.

There, the hard work is done. Leave the remaining to Sage!

Obtain the characteristic polynomial of the matrix, which also is the characteristic equation of the required recurrence equation.

am=matrix([
[0, 7, 1, 1, 0, 0],
[0, 8, 1, 1, 0, 0],
[0, 8, 1, 0, 1, 0],
[0, 8, 0, 1, 0, 1],
[0, 8, 0, 0, 0, 1],
[0, 7, 1, 0, 1, 0]
])
print am.characteristic_polynomial()

The characteristic equation is:

\begin{equation*} \displaystyle x^{5} - 10x^{4} + 2x^{2} - 1 = 0 \end{equation*}

So, the recurrence would be:

\begin{align*} \displaystyle a_{i+5}&=10\, a_{i+4}-2\, a_{i+2}+a_{i} \\ a_{0}&=1\\ a_{1}&= 9\\ a_{2}&= 90\\ a_{3}&= 898\\ a_{4}&= 8962\\ \end{align*}

Wonder if anyone can come up with a combinatorial argument for that equation?!

Initial conditions can be easily obtained by matrix exponentiation or using a program to iterate through the sequences, e.g.

1	print sum((am^4)[0,:].list())

cnt = 0
for i in range(1000,10000):
    if str(i).find('122')==-1 and str(i).find('213')==-1:
        cnt += 1
print cnt

We can also automatically get the generating function of the obtained recurrence by using a small program (method is given in "Lectures on generating functions" by S. K. Lando):

def get_gf(alst,initvals):
    nn=len(alst)
    Am = zero_matrix(QQ,nn-1,1).augment(identity_matrix(nn-1)).stack(matrix(QQ,alst[::-1]))
    Bm = matrix(QQ,initvals)
    return (((identity_matrix(nn)-x*Am).inverse()*Bm.transpose())[0,0]).full_simplify()
print get_gf([10,0,-2,0,1],[1,9,90,898,8962])

which gives the g.f.

\begin{equation*} \displaystyle G(x)=\frac{x - 1}{x^{5} - 2 \, x^{3} + 10 \, x - 1} \end{equation*}

There are tremendous uses of generating functions, one of which is to obtain an asymptotic formula. (See William Feller's book on probability for a brief explanation on the topic)

If we have a generating function of the form \(G(x)=U(x)/V(x)\), then the asymptotic form is given by

\begin{equation*} \displaystyle a_n \sim \dfrac{\rho_1}{s_1^{n+1}} \displaystyle \textrm{where }\rho_1=\dfrac{-U(s_1)}{V^{'}(s_1)} \displaystyle \textrm{and }s_1 \textrm{ is the root of }V(x)\textrm{ nearest to origin} \end{equation*}

We will visually inspect where the roots lie, to get an idea about the closest root to the origin

1	complex_plot(x^5 - 2x^3 + 10x - 1,(-2, 2), (-2, 2))

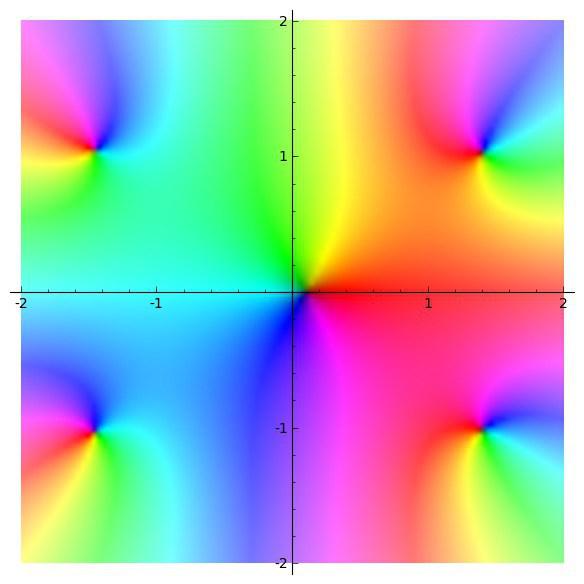
complex plot of the equation

and we see that there is only one real root (also the nearest to origin) and other four are complex.

We can proceed with the following steps in Sage:

s1=find_root(x^5 - 2*x^3 + 10*x - 1, 0, 4)
rho1=(1-s1)/diff(x^5 - 2*x^3 + 10*x - 1,x).subs(x=s1)
f(n)=rho1/s1^(n+1)
print int(f(15)),f(n)

We find the approximation to be

\begin{equation*} \displaystyle a_n \sim \frac{0.0905207193521}{0.100200193518^{n + 1}} \end{equation*}

The \(15^{th}\) term using the asymptotic formula gives about \(876700051238642\), which is only a little more than the actual value of \(876700051238641\).